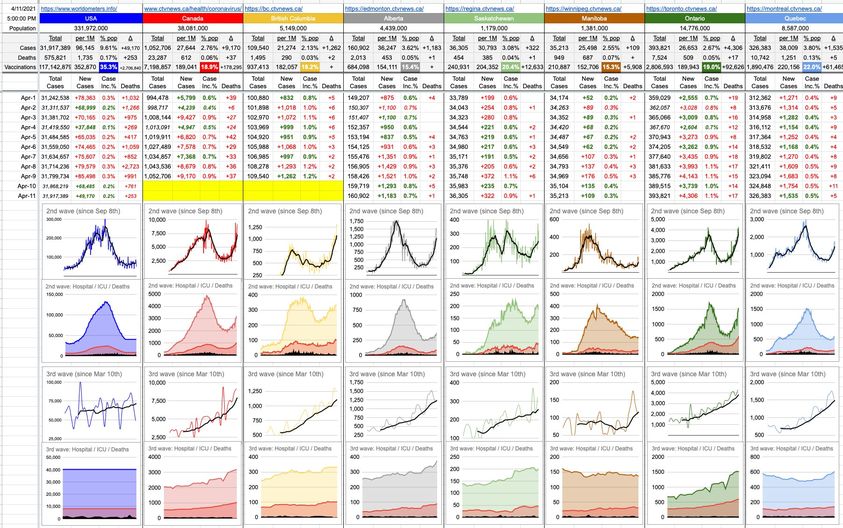
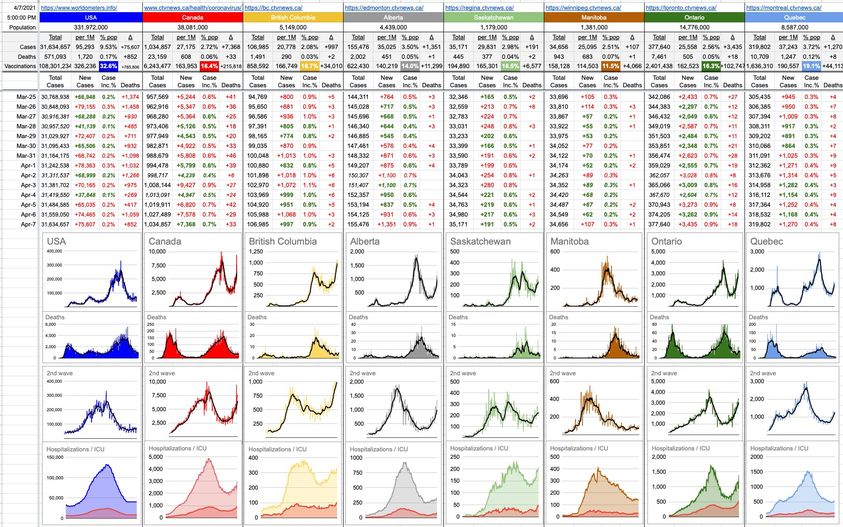
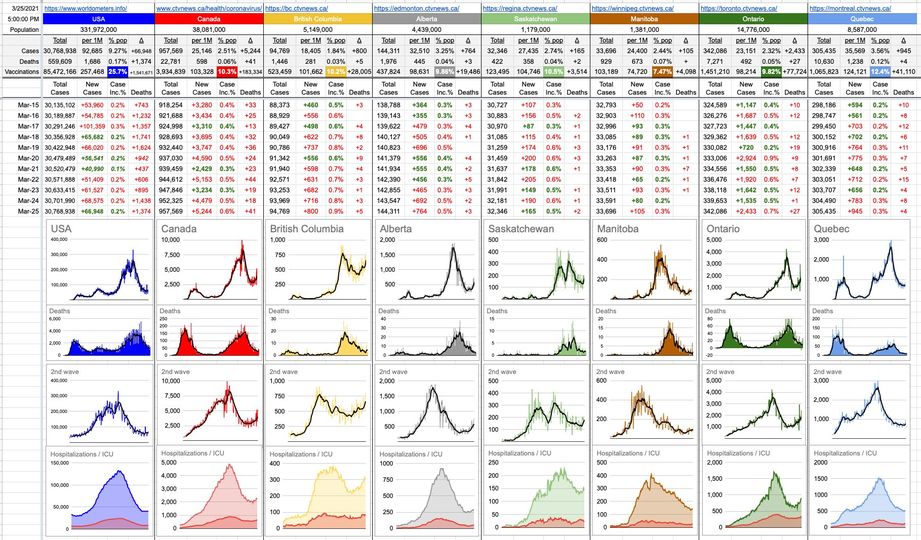
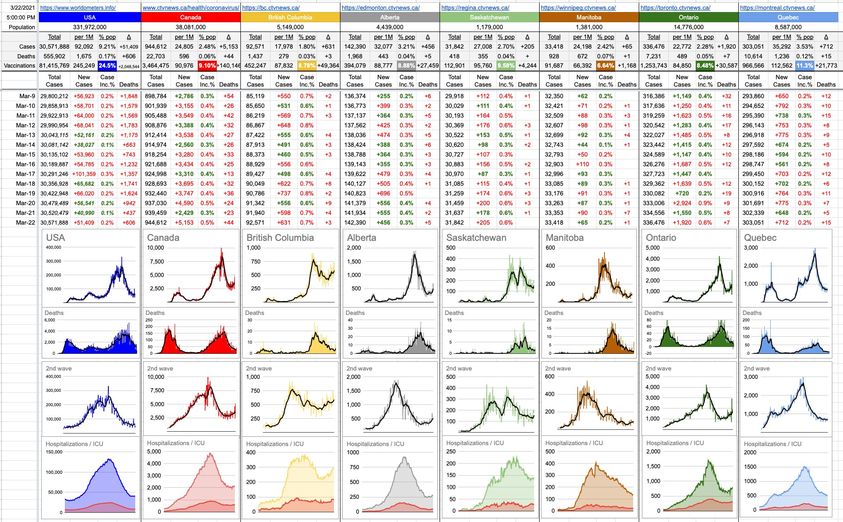
Imagine a big map of North America… now, take 100 pins and stick then on the 100 biggest cities. Now imagine trying to find the shortest path that visits every city exactly once. Imagining the problem isn’t difficult. Solving it is a different story.
To solve it, you’d create a table of all the distances from once city to another. Each city would have a list off 99 entries below it… Vancouver to Seattle, Vancouver to Portland, Vancouver to Miami… etc. The total number of distances to consider would be 100 x 99… and yes, even though Vancouver to Seattle is the same as Seattle to Vancouver, you need the entry twice in the table because, in the solution, you’re not sure from which direction you’d be approaching.
Setting up a computer to solve this is simple: Generate every version of path through all cities, add up the little distances, and keep track of the best one so far. Once you’ve cycled through all the combinations, you’ll have the answer. This is easy, in theory.
It gets a bit more complicated in practice.
How many combinations of paths are there? Starting in any city, there are 99 options for the next one. Once you get there, there are 98 choices for the next one. After that, 97. Therefore, the number of combinations is 100 x 99 x 98 x… all the way down to x 1. That’s 100 factorial (100!) which equals… a really big number. How big? It’s a number with 157 zeroes after it. The number of particles in the universe is a number with 80 zeroes after it. How long would it take to analyze every combination? A few zillion years. Not too practical. That’s how long it’d take to find the perfect solution… but how about a “good enough” solution? Not 100%, but how about 95%?
Back in 1993, when I wrote a program like this, it took about 20 minutes. With today’s horsepower, any home computer could do it in less than a minute.
That’s quite a difference, and for all practical purposes, good enough. The traveling salesman can spend a few extra days on the road and burn a bit more gas… not a big deal. Good enough.
One strategy to solve big problems down to a “not perfect but good enough” level is what’s called a “Genetic Algorithm”… it’s what I used, and it’s pretty cool, so now you get to hear about how it works.
Out of the zillions of possible 100-city-tours, imagine you generate a bunch of random ones… say 10,000 of them. Just create 10,000 unique paths through those 100 cities, totally randomly. Some, like the ones that begin Vancouver-Miami-LA-Toronto… will be awful. Ones that start Vancouver-Seattle-Portland are likely to look better. But… whatever they look like, out of the 10,000… take the best 100.
Now… here comes the cool part… you take those 100 – call them the “first” generation, and figuratively “breed them” to each other. You pretend they’re like parents having offspring… you splice half of one, splice half of another, join them together… and now you have a whole new potential solution. It might be better than one or both parents… it might be worse. Doesn’t matter… breed all the combinations… now you have a whole new generation of 10,000 possible solutions, and they’re almost all certain to be better than their respective “parents”. And now you take the best 100 of those and do it again, and create a third generation. This is like instant evolution… but it doesn’t take 9 months and lots of diapers. It takes a few milliseconds… and that’s the beauty of it… after less than 1,000 generations, which doesn’t take long at all, you have a surprisingly good solution. Already north of 90%.
Modelling 100 cities with nothing but the distances between them is very simple. Modeling the infrastructure within which a virus may live and thrive and propagate is a lot more complicated, but once it’s in place, searching for a solution might look similar. Here’s a random formula for a mRNA vaccine… was it effective? Try 10,000 random formulas, pick the best 100… splice them, mix them, test them… and do it again. And again and again. Pretty quickly, you will have honed-in on realistic possibilities.
This isn’t quite how it came about… but when people wonder how it’s possible to come up with an answer to a supremely complicated and unknown problem, it’s strategies like this… which have the capability of very-quickly zeroing in on viable solutions drawn from an unfathomably huge search-space of potential solutions.
Finding the perfect vaccine might take decades… if not centuries. But a vaccine doesn’t have to be perfect.
How long would it take to find one that’s good enough… say, 95% effective…?
That question has been answered.

14 Likes, 3 Shares